The basic relationship, WIP = CT x TH known as Little’s Law has wide application in both production systems as well as projects [1]. However, when some parts/tasks are never completed because they are either scrapped (yield loss) or have become obsolete (as in a project), the application becomes a bit more complex. This study presents an analysis of these situations and concludes with a more general set of Little’s Law equations, as referenced in Factory Physics [2].
Keywords: Little’s Law; WIP; Throughput; Cycle Time; Variability; Yield Loss
Little’s Law [1, p. 239] describes the relationship between the Work-In-Process (WIP), Cycle Time and Throughput for an individual operation, and also for an entire production system composed of a set of operations. The law, as stated, assumes that inputs into an operation are perfectly transformed into outputs, all of which move to the next operation. For instance, the idealized production system illustrated in Figure 1 shows a sequence of operations or steps that must be executed. Each step i has a cycle time ti , throughput THi and is preceded by WIPi. The output of the i-th step goes entirely into the WIP of the i+1st step. Under these conditions, Little’s Law holds for each step WIPi = ti x THi I as well as for the overall production system.

Figure 1: An Idealized Production System
In real production systems, production operations may not have 100% perfect output. In practice, at step i, there will be a useful yield fraction yi. which goes on to the successor step i+1, with a fraction (1-yi ) lost immediately after step i. Using Little’s Law and accounting for the yield that passes from step i to step i+1, the WIP preceding step i+1, WIPi+1 = yi THi ti .
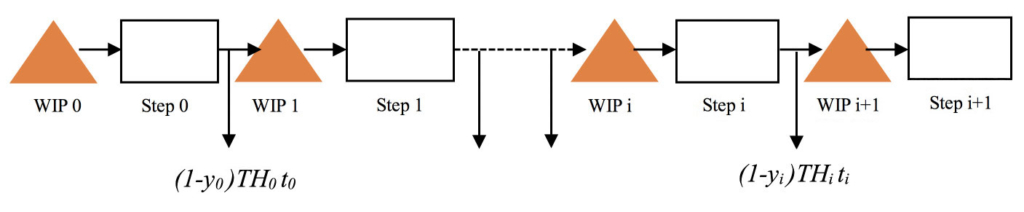
Figure 2: Production system with yield losses
Using the yields yi, we can extend the relationships between successive steps to cycle time statistics involving only those parts that have been completed for the entire production system. To do this, we must consider both yielded and observed cycle times, throughput and WIP. Before we derive the relations between yielded quantities, we summarize some notation based on the terminology we have already introduced.
Let:

The average observed cycle time is simply the sum of the average cycle times at each step. In other words:
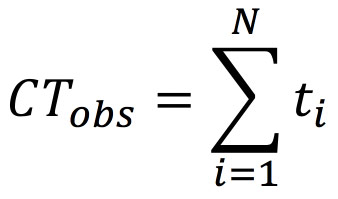
The average yielded cycle time is a similar sum but multiplied by the yield at each step, thereby capturing only the cycle time that made it to that step:
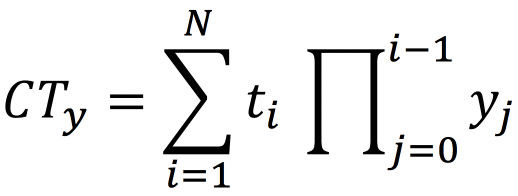
The yielded WIP will be the sum of the local throughput times the average cycle time.
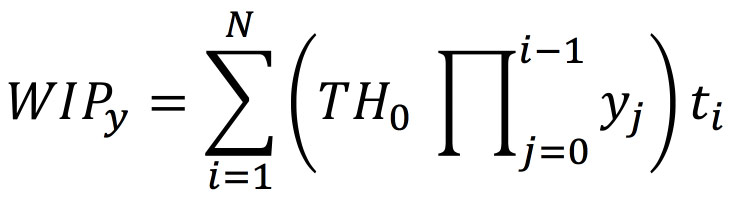
But this is simply,
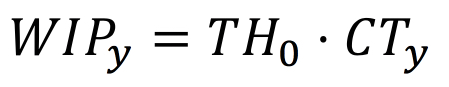
Note that the observed WIP (i.e., what we see in the fab) is already yielded. In other words, if it has fallen out, we would not see it in the fab. Thus,
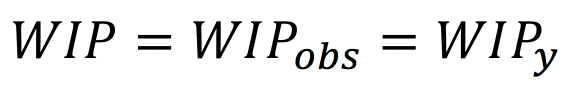
Throughput is a bit more complex, as there is starting throughput, ending throughput and yielded throughput. Ending throughput is simply the starting throughput times the “rolled throughput yield,” Y. This must be equal to the demand for the product, D. So, the relationship between the starting throughput, THo, and the demand is:
![]()
The yielded throughput is the average throughput weighted by the cycle time at each step:
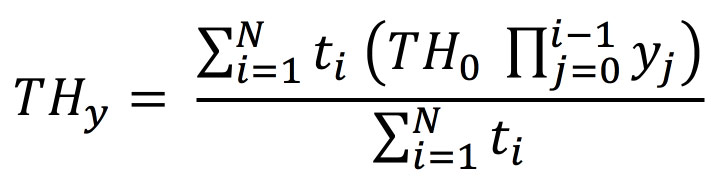
But this is simply:
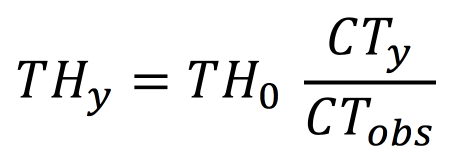
or,
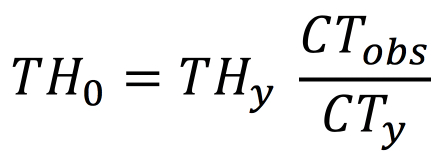
We can now rewrite Little’s Law in terms of observed and yielded quantities:
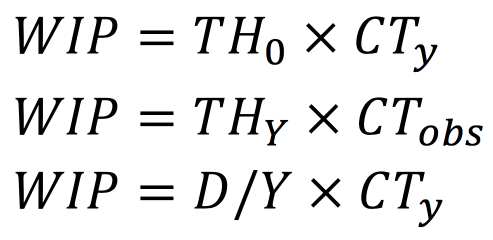
If any of the yields of the process are less than 100%, we know that Y < 1 and THy > D. Consequently,
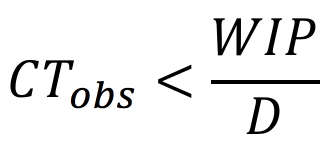
We can compute a tighter upper bound on observed cycle time for a special case that is similar to many situations found in industry.
Consider if the case were ti = t and yi = y for all i. In this case,
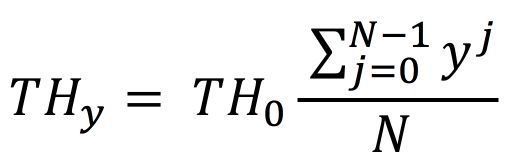
It can be shown that.
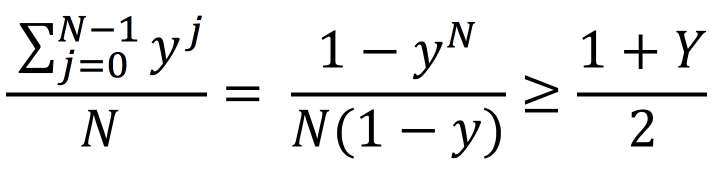
Or,
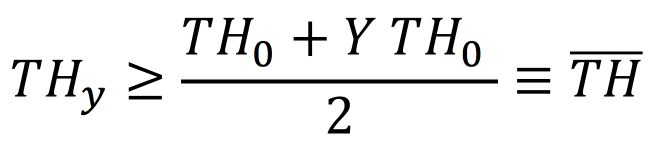
So that,
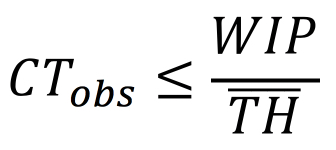
This bound should hold if both the yields and local cycle times are fairly uniform. Consequently, it is pretty easy to obtain an upper bound for observed cycle time by knowing demand, overall yield and average observed WIP.