Simulation Preemption of Construction Operations

Introduction

Preemption is the interruption of an activity in progress while a simulation is running and the reallocation of the preempted activity’s resources to another activity that is started at that time [1]. In STROBOSCOPE [2], preemption is the immediate termination of an activity instance that currently resides in the Future Event List (FEL) and the start of a new instance of some other activity that takes over all the resources of the preempted instance. Presented below are the new preemption functions and statements that have been added to the STROBOSCOPE simulation system. These new preemption capabilities are illustrated through their application to two examples. Due to space limitations, only the new statements and functions related to preemption are described. Identifiers chosen by the user are shown in italics, such as “Load” in “Load.TotInst.-1”, while regular text shows STROBOSCOPE identifiers that must be entered as shown. More information about the STROBOSCOPE language is found in [3].

New Stroboscope Functions and Events to Support Preemption

Interrupting an Activity in Progress — The “Preempt” Function

Preemption has been implemented in STROBOSCOPE through the new function Preempt that can be called at appropriate trigger events while a simulation model is running to interrupt an activity instance currently in progress. The syntax of the function Preempt and the actions it takes are summarized below.

Syntax:  Preempt[CurAct, InstNum, NewAct]
Example: Preempt[Load, Load.TotInst-1, StopLoad]
Returns: Either the value 1 (success) or the value 0 (failure)

When the function Preempt is called, it takes the following actions:

• It scans the Future Event List (FEL) to find the instance of activity CurAct (e.g., Load) whose instance number (i.e., 0, 1, 2, …) is given by the number InstNum. For example, Load.TotInst-1 is the number of the last instance of Load that has been created. It should be noted that the instances of an activity are given consecutive integer numbers with the first instance having the number 0. The global variable CurAct.TotInst returns the total number of instances of a activity CurAct up to now, and thus its last instance has the number CurAct.TotInst-1 and can be preempted by Preempt[CurAct, CurAct.TotInst-1, NewAct].
• If the instance of activity CurAct with number InstNum is not found in the FEL, then the function Preempt stops and returns the value 0 (false) to indicate failure.
• If the instance of activity CurAct with number InstNum is found in the FEL, then the function Preempt continues and creates a new instance of activity NewAct (whose instance number is NewAct.TotInst-1) that takes over all the resources of the preempted instance of activity CurAct.
• The duration of the new instance of activity NewAct is set equal to the remaining duration of the preempted instance of CurAct.
• The statistics for activity CurAct are corrected by un-collecting the original duration of the preempted instance and collecting its truncated duration.
• Instance number InstNum of activity CurAct is terminated and the function Preempt stops and returns the value 1 (true) to indicate success.

Because the function Preempt is a logical function that returns the value 1 to indicate success or the value 0 to indicate failure, it can be used in the logical expressions that control the actions of other statements. In the models that follow, for example, the function Preempt is used in the logical preconditions that determine whether event actions will actually take place at certain events during simulation.

Resetting the Duration of an Existing Activity Instance — The “SetTmLeftInst” Function

By default, when the function Preempt creates a new instance of activity NewAct (with instance number NewAct.TotInst-1) it sets its duration equal to the remaining duration of the preempted instance of CurAct (with number InstNum). Oftentimes, however, this is not the appropriate duration required by the model.

The new function SetTmLeftInst can be called at appropriate events during simulation to reset the remaining duration of any activity instance that is currently in progress to any desired value. The syntax of the function SetTmLeftInst and the actions it takes are summarized below.

Syntax:  SetTmLeftInst[Activity, InstNum, RemDur]
Example: SetTmLeftInst[StopLoad, StopLoad.TotInst-1, 0]
Returns: Either the value 1 (success) or the value 0 (failure)

When the function SetTmLeftInst is called, it takes the following actions:

• It scans the Future Event List (FEL) to find the instance of Activity (e.g., StopLoad) whose instance number is InstNum. For example, StopLoad.TotInst-1 will find the last instance of StopLoad.
• If an instance of Activity with number InstNum is not found in the FEL (because it was never created or it has already finished), then the function SetTmLeftInst stops and returns 0 (false).
• If the instance of Activity with number InstNum is found in the FEL, then the function SetTmLeftInst changes the instance’s duration to RemDur and corrects its end-event time in the FEL so that the instance will now finish at SimTime + RemDur.
• The duration-related statistics for Activity are corrected by un-collecting the instance’s original duration and collecting its new duration RemDur.
• The function SetTmLeftInst ends and returns the value 1 (success).

Like the function Preempt, the function SetTmLeftInst is a logical function that returns the value 1 or the value 0 and can be used in logical expressions to control other statements in the model.

New Action Events Related to the “Preempt” Function

When an activity instance is preempted successfully, it is often necessary to take additional actions— for example, to store new values in global SaveValues or to store new data in the private SaveProps of specific characterized resources. The following two new action events occur only if the function Preempt is successful. These events occur after the function Preempt has found the instance to preempt in the FEL, and before the function Preempt finishes and returns the value 1 (success).

Syntax:  BEFOREPREEMPTED  CurAct  [Action]  ActionTarget  TargetArgs;
Timing:  Occurs after the function Preempt has corrected the duration-related statistics of CurAct and before the current instance count of CurAct is reduced by one.

Syntax:  AFTERPREEMPTING NewAct  [Action]  ActionTarget  TargetArgs;
Timing:  Occurs after the preemption of CurAct is complete and after the new instance of NewAct has been created and has taken over the preempted resources and the remaining duration of CurAct.

The action events BEFOREPREEMPTED or AFTERPREEMPTING can be triggered by the action event for another activity that calls the function Preempt (such as, BEFOREEND TriggerAct). In this case, both the instance of TriggerAct and the instance of CurAct (or NewAct) are in context. This is important because in this situation the attributes and resources of both the instance of TriggerAct and the instance of CurAct (or NewAct) are accessible, such as through the new activity instance variable Activity.StartTm described next.

Accessing the Start Time of an Activity Instance — “Activity.StartTm” Instance Variable

It is often necessary to access the start time of a particular instance of an activity that is currently in context in order to calculate, for example, the duration of that instance up to the current simulation time, or to use this start time to set the properties (such as the duration) of another activity instance later.

The new instance variable Activity.StartTm provides the start time of any activity instance (such as CurAct or NewAct) that is currently in context. When an activity instance is in context, the system can determine unambiguously which of the several instances of Activity that may be in progress is being referenced.

The global variable Activity.LastStart, though similar, has a different purpose. It can be used at any time to return the start time of the last instance of Activity that has been created, even if that last instance is not in context, or has already finished. In contrast, the instance variable Activity.StartTm can return the start time for any instance of Activity that is in progress and in context (and not necessarily just the last one).

Appropriate uses of the instance variable Activity.StartTm, as well as applications of the new preemption functions, Preempt and SetTmLeftInst, and the new action events BEFOREPREEMPTED and AFTERPREEMPTING are illustrated by the following two example models.

Simulation of Moving Soil by Wheelbarrow

In this apparently simple example, two laborers use two 6-cf wheelbarrows to move soil. The Load activity uses the first laborer (the Loader) to load one of the wheelbarrows with soil. The Haul activity uses the other laborer (the Hauler) to push a loaded wheelbarrow, dump the soil, and return the empty wheelbarrow to load again. The durations of the Load and Haul activities L and H (in minutes) are balanced and follow normal distributions with the same mean value, 2 min. However, they have different standard deviations SD[L] and SD[H]. This example investigates whether the deliberate preemption of the Load activity by the Haul activity can be beneficial by varying the standard deviations SD[L] and SD[H] and comparing the long-term production (in cf/min) of the following two policies A and B.

Policy A: A wheelbarrow can be hauled only when fully loaded with 6 cf of soil. When activity Haul finishes first, it waits for activity Load to finish before both can start again.

Policy B: If a wheelbarrow is still being loaded when activity Haul finishes, then loading that wheelbarrow stops, and Load starts again with the empty wheelbarrow that has just arrived. At the same time, the Haul activity starts again with the partially loaded wheelbarrow whose load is 6 cf times its truncated load time over the total time that would have resulted in a complete load of 6 cf.

WheelBarrow Cycle Analysis

For both policies A and B, activities Load and Haul start at the same time in every cycle but have different durations L and H (in minutes). The two policies also have different cycle times. The cycle time for policy A is max(L, H) whereas the cycle time for policy B is H.

For each policy, the production in each cycle r(A) and r(B) (in cf/min) depends on whether L < H or L > H.

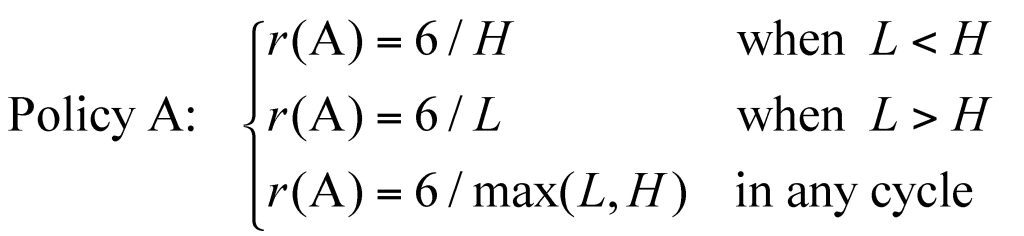
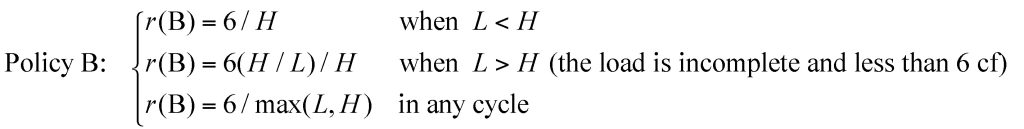
This analysis shows that the productions in each cycle r(A) and r(B) (in cf/min) for the two policies are identical and equal to 6/max(L, H) = min(6/L, 6/H). The difference is that under policy B some cycles carry less than 6 cf of soil, but also take less time. Based on this, the two policies would appear to be equivalent. However, the long-term productions for the two policies, R(A) and R(B) (in cf/min), that are given by the ratio of the total volume of soil moved in n cycles over the total time of n cycles are quite different.

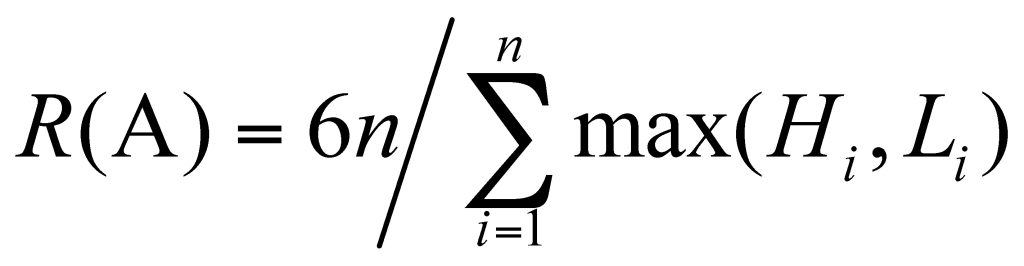
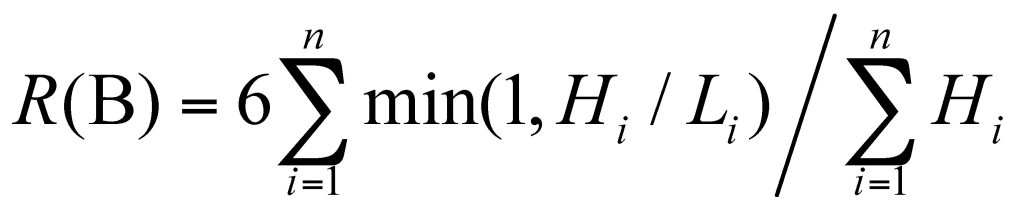
Clearly, the long-term productions R(A) and R(B) over n cycles are random variables given by different functions of the random variables L and H and cannot be compared analytically. A meaningful comparison of the long-term productions of policies A and B over n cycles is by simulation that uses both preemption and the common random numbers variance reduction technique [4].

STROBOSCOPE Simulation Model for Policies A and B

The STROBOSCOPE simulation model network for moving soil by wheelbarrows is shown in
Figure 1. Described below are the new STROBOSCOPE statements that are needed to implement the preemption of activity Load by activity Haul. (The complete models presented here are available from the author.)

The model begins by defining the SaveValue HaulPreemptsLoad that controls which policy, A or B, will be simulated by the model.

SAVEVALUE HaulPreemptsLoad 1; / Changes policy: 0 → A (No Preemption), 1 → B (Preemption)

Three types of resources are defined. Laborer and Soil are modeled as generic resources. WheelBarrow is modeled as a compound resource with one SaveProp named AmountLoaded that will store the amount of soil currently loaded in the WheelBarrow.

GENTYPE  Laborer;  GENTYPE  Soil;

COMPTYPE  WheelBarrow;  SAVEPROP  WheelBarrow  AmountLoaded;

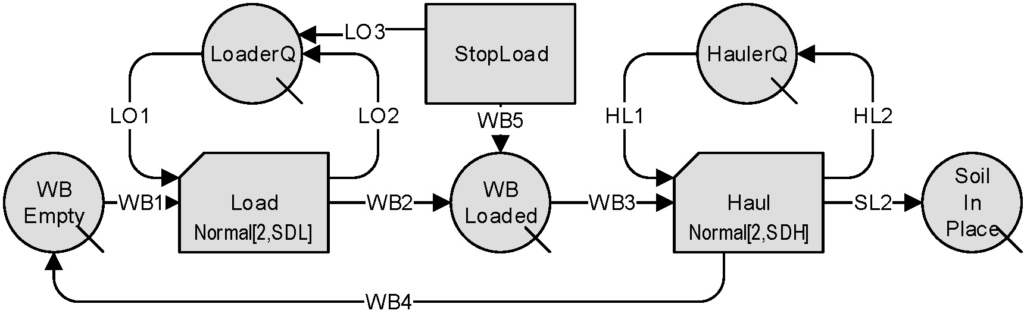
Each time an instance of activity Load starts, it stores 6 cf of soil in the SaveProp AmountLoaded of the WheelBarrow resource that is currently inside that Load instance. If this Load instance is later preempted, then the AmountLoaded in the WheelBarrow will be adjusted to less than 6 cf at the time of preemption.

ONSTART  Load  ASSIGN  Load.WheelBarrow.AmountLoaded  6;

Right before an instance of activity Haul ends, it attempts to call the function SetTmLeftInst. This call takes place only if its two logical preconditions (PRECOND) are satisfied. The first is that HaulPreemptsLoad has the value 1. The second is that the function Preempt can successfully preempt the last instance of activity Load and create a new instance of activity StopLoad that takes over the resources (a WheelBarrow and a Laborer) and the remaining duration of the preempted instance of Load. If both preconditions return the value 1 (true), then the function SetTmLeftInst is called and resets the duration of the new instance of activity StopLoad to zero so that both Load and Haul can start immediately.

BEFOREEND  Haul  CALL
    PRECOND ‘HaulPreemptsLoad & Preempt[Load, Load.TotInst-1, StopLoad]’
       ‘SetTmLeftInst[StopLoad, StopLoad.TotInst-1, 0]’;

The following statement shows an example of the new event BEFOREPREEMPTED which occurs only if the instance of activity Load is indeed preempted. In that case, the wheelbarrow is loaded with less than 6 cf and the action taken is to adjust the SaveProp AmountLoaded in the WheelBarrow accordingly.

BEFOREPREEMPTED Load   ASSIGN Load.WheelBarrow.AmountLoaded
                       ‘6 * (SimTime - Load.StartTm) / Load.Duration’;

In the above statement, the new instance variable Load.StartTm returns the start time of the instance of Load being preempted (and which is currently in context). Subtracting it from the current simulation time SimTime gives the instance’s truncated duration. The instance variable Load.Duration returns the original duration of the preempted instance of Load that would have resulted in 6 cf being loaded into the wheelbarrow. Thus, 6 cf times the ratio of the truncated duration of the preempted instance of Load divided by its original duration gives the current amount of soil in the partially loaded wheelbarrow.

STROBOSCOPE Simulation Results

The STROBOSCOPE model compares the long-term productions R(A) and R(B) for Policies A and B, and calculates their difference R(B)-R(A), using the common random numbers variance reduction technique that compares the performance of the two alternatives under identical random number streams and thus under identical streams of the durations L and H of activities Load and Haul [4]. The resulting difference in production R(B)-R(A) in cf/min is shown in Figure 2.

Figure 2 shows that R(B)-R(A) is positive towards the left, negative towards the right, and close to zero along the front-to-back diagonal. Thus, the deliberate preemption of activity Load by activity Haul does improve long-term production, R(B) > R(A), when SD[H] < SD[L], i.e., when the duration of activity Haul has less variability than the duration of activity Load.

This interesting result suggests that when two balanced activities interact (such as Load and Haul), it may be beneficial to keep the activity with the less variable duration working continuously (such as Haul when SD[H] < SD[L]) by interrupting if needed (and if possible) the other activity (e.g., Load) that has a more variable duration. Clearly, this is not always possible as activity Load, for example, cannot interrupt activity Haul. Nevertheless, when activity Load is less variable than activity Haul, SD[L] < SD[H], then activity Load should be kept working as continuously as possible and should not be preempted by activity Haul. This is an interesting observation that merits further investigation.

Unloading Fill Material From Barges Using Two Cranes

In this example, barges carrying construction fill material for undersea land reclamation arrive at the unloading facilities of a harbor. The interarrival times between barges are independent and exponentially distributed random variables with a mean of 1.25 days. The harbor has a dock with two berths and two cranes for unloading the fill material from the barges. When both berths are occupied, arriving barges join a first-in-first-out (FIFO) queue. The time for one crane to unload a barge is uniformly distributed between 0.5 and 1.5 days. When two barges are available to unload, then each barge is unloaded by one crane. When only one barge is available to unload, then both cranes can work on the same barge and its remaining unload time is cut in half. In this case, the arrival of a second barge at the other berth switches unloading back to each barge using one crane, and the remaining unload time for the first barge is doubled. The unloading of a barge can switch several times between using one or two cranes, with corresponding adjustments to its remaining unload time. This makes the unloading operation significantly more difficult to model without the new preemption facilities added to STROBOSCOPE.

Simulation Model—Unloading may be Preempted Multiple Times

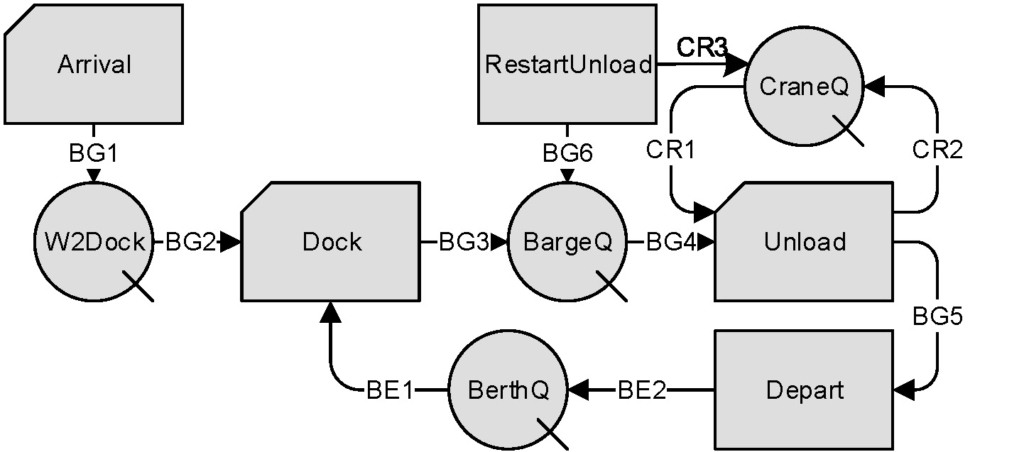
The network for the STROBOSCOPE simulation model is shown in Figure 3. The STROBOSCOPE statements needed to implement preemption are described below.

Three types of resources are needed. Berth and Crane are generic resources. Barge is a compound resource with three SaveProps. RemUnloadDur stores the remaining unload duration if the work is done by a single Crane. TimesPreempted stores the number of times that the Barge was preempted. CraneSeq stores a number made up of the digits 1 and 2 that reflects the sequence of Cranes (1 or 2) that unloaded the Barge.

GENTYPE   Berth;  GENTYPE    Crane;
COMPTYPE  Barge;  SAVEPROPS  Barge  TimesPreempted  CraneSeq;

The following Semaphore ensures that activity Arrival can only have one instance going on (this instance starts as soon as the previous instance of Arrival ends). Its duration is
exponentially distributed.

SEMAPHORE   Arrival  ‘!Arrival.CurInst’; /One Arrival at a time
DURATION    Arrival  ‘Exponential[1.25]’;

Each arriving resource of type Barge is created dynamically right before each instance of activity Arrival ends. The time needed to unload the Barge by a single Crane working alone is sampled from a uniform distribution and is stored in its SaveProp RemUnloadDur when the Barge is released though link BG1.

BEFOREEND   Arrival  GENERATE   1 Barge;
ONRELEASE   BG1      ASSIGN RemUnloadDur     ‘Uniform[0.5, 1.5]’;

An arriving Barge waits in the FIFO queue W2Dock. When one of the two Berths becomes idle in BerthQ, activity Dock creates an instance that transfers the Barge to the queue BargeQ (which at most contains the two Barges that are currently unloading). When a Barge is released to the queue BargeQ through link BG3, it attempts to call the function SetTmLeftInst and possibly preempt the ongoing instance of activity (but only if the ongoing instance of Unload is currently using both Cranes).

ONRELEASE   BG3   CALL
  PRECOND ‘!CraneQ.CurCount &
    Preempt[Unload, Unload.TotInst-1, RestartUnload]’
     SetTmLeftInst[RestartUnload, RestartUnload.TotInst-1, 0];

The above call to the function SetTmLeftInst takes place only if its two logical preconditions 104 (PRECOND) return the value 1 (true). The first precondition checks whether there are no idle Cranes in CraneQ. If true, this means that the last instance of activity Unload is using both Cranes and should be preempted so that the unloading of the preempted Barge can continue with one Crane, while the second freed Crane can start unloading the Barge that has just docked at the Berth. The second precondition calls the function Preempt to interrupt the last instance of activity Unload and transfer its resources (one Barge and two Cranes) and its remaining duration to a new instance of activity RestartUnload. If both logical preconditions return the value 1 (true), then the function SetTmLeftInst sets the duration of the new instance of RestartUnload to zero so that the two Cranes and the partially unloaded Barge will be released back to their queues CraneQ and BargeQ and allow two new instances of activity Unload to start immediately (one with the existing Barge and the other with the Barge that has just docked at the Berths).

Whenever an instance of activity Unload is preempted, it is also necessary to adjust the time needed for a single Crane to finish unloading the Barge. This time (which is stored in the SaveProp RemUnloadDur) is reduced by the elapsed duration of the preempted instance of activity Unload times the number of Cranes (1 or 2) that were unloading the Barge.

BEFOREPREEMPTED   Unload  ASSIGN Unload.Barge.RemUnloadDur
     ‘Unload.Barge.RemUnloadDur - (SimTime - Unload.StartTm) * Unload.Crane.Count’;

Similarly, whenever an instance of activity Unload is preempted, the total number of times that the Barge has been preempted (which is stored in the SaveProp TimesPreempted) is increased by 1.

BEFOREPREEMPTED.  Unload  ASSIGN Unload.Barge.TimesPreempted
    ‘Unload.Barge.TimesPreempted + 1’;

The current sequence of the number of Cranes (1 or 2) that worked alone or together to unload a Barge is stored in the SaveProp CraneSeq as a number that consists only of the digits 1 and 2. For example, the CraneSeq final value 1212 indicates that the Barge started unloading with one Crane, continued with two Cranes, switched back to one Crane, and finished unloading with two Cranes. The number stored in CraneSeq is updated whenever an instance of activity Unload is preempted and when it ends normally.

BEFOREPREEMPTED    Unload  ASSIGN Unload.Barge.CraneSeq
    ‘Unload.Barge.CraneSeq*10 + Unload.Crane.Count’;
BEFOREEND    Unload  ASSIGN Unload.Barge.CraneSeq
    ‘Unload.Barge.CraneSeq *10+ Unload.Crane.Count;

When an instance of activity Unload that was using both Cranes is preempted (because a new Barge has arrived at the Berths), its Barge flows through an instance of activity RestartUnload with zero duration and immediately enters queue BargeQ. At that point, BargeQ will contain both Barges currently docked at the Berths (the Barge that was preempted and the Barge that just arrived). The following discipline statement will place at the front of the queue BargeQ the Barge with the shortest remaining unload time RemUnloadDur. Thus, when the Barge that finishes unloading first departs, the Barge still unloading will be in the last instance of Unload and can possibly be preempted later (as described below).

DISCIPLINE    BargeQ  ‘RemUnloadDur’;

A new instance of activity Unload draws first a Barge from BargeQ and then Cranes from CraneQ. This way, the number of Cranes drawn (1 or 2) can depend on the remaining contents of queue BargeQ. If there are any Barges in queue BargeQ waiting to unload, then link CR1 should draw only one Crane. Otherwise, it draws all available Cranes (i.e., two Cranes) and passes them to the starting instance of activity Unload.

DRAWAMT   CR1  ‘BargeQ.CurCount? 1 : CraneQ.CurCount’;

After a new instance of activity Unload draws resources, it determines its duration by dividing the SaveProp RemUnloadDur of the Barge that it has already drawn by the number of Cranes (1 or 2) that it has also drawn and which will work together to unload the Barge.

DURATION   Unload  ‘Unload.Barge.RemUnloadDur / Unload.Crane.Count’;

The activity Depart is a dummy activity with zero duration that occurs when a Barge finishes
unloading and leaves the harbor. When an instance of Depart starts, it attempts to call the function SetTmLeftInst when all three of the logical preconditions for the call action return the value 1 (true).

ONSTART Depart CALL
    PRECOND ‘Unload.CurInst & !W2Dock.CurCount &
    (Preempt[Unload, Unload.TotInst-1, RestartUnload] | Preempt[Unload, Unload.TotInst-2, RestartUnload])’
      ‘SetTmLeftInst[RestartUnload, RestartUnload.TotInst-1, 0]’;

The first precondition checks that activity Unload does have a current instance. The second precondition checks that the queue W2Dock is currently empty. I.e., that there are no Barges waiting to unload (other than the Barge inside the ongoing instance of activity Unload). And the third precondition attempts to preempt the last or the next-to-last instance of activity Unload and start a new instance of RestartUnload.

If all three preconditions return the value true, then the function SetTmLeftInst is called to set the duration of the new instance of RestartUnload to zero. Preempting the ongoing remaining instance of Unload (when the unloading Barge is the only one left in the harbor) allows activity Unload to start again and create a new instance that will use two Cranes, the preempted Crane (that will become available immediately) and the Crane that just finished unloading the departing Barge.

The reason that the above statement includes the second call to the function Preempt (that preempts the next-to-last instance of activity Unload with instance number Unload.TotInst-2) is because despite the discipline of queue BargeQ that attempts to sort the unloading Barges (and thus the current instances of Unload that start at the same time) based on which instance will finish first, it is still possible that the last instance of activity Unload may finish first and before the next-to-last instance of Unload.

This can occur under the following sequence of events. Suppose that activity Unload has two instances currently going on (both using 1 Crane), Unload(x) and Unload(x+1). Unload(x) finishes and its Barge departs. No preemption takes place because another Barge in queue W2Dock is waiting to unload. The new Barge starts Unload(x+2) with 1 Crane. Then, Unload(x+1) finishes and its Barge departs. Again, no preemption takes place because another Barge in queue W2Dock is also waiting to unload. This new Barge starts Unload(x+3) with 1 Crane. At this point, activity Unload has two instances going on at the same time, Unload(x+2) and Unload(x+3), both using 1 Crane. These two instances started at different times, they were never preempted, and their Barges were never in BargeQ at the same time. Thus, the discipline of queue BargeQ did not sort the unloading Barges (and thus the instances Unload(x+2) and Unload(x+3)) based on which instance would finish first. Due to randomness in sampling, it is possible that although Unload(x+3) started after Unload(x+2), it may finish first, before Unload(x+2) finishes. If no other Barge is currently waiting to unload in queue W2Dock when Unload(x+3) ends and activity Depart starts, the first call to the function Preempt will attempt to preempt the last instance Unload(x+3) that has just finished and will fail. Thus, the second call to the function Preempt is needed to preempt successfully the next-to-last instance Unload(x+2) that is still going on and is still in the FEL. It should be noted that because the operator between the two calls to the function Preempt is a logical “OR”, “|”, the second call to the function Preempt is made only if the first call fails and returns the value false. The fact that the first call to the function Preempt may fail has no detrimental effects on the model.

STROBOSCOPE Simulation Results

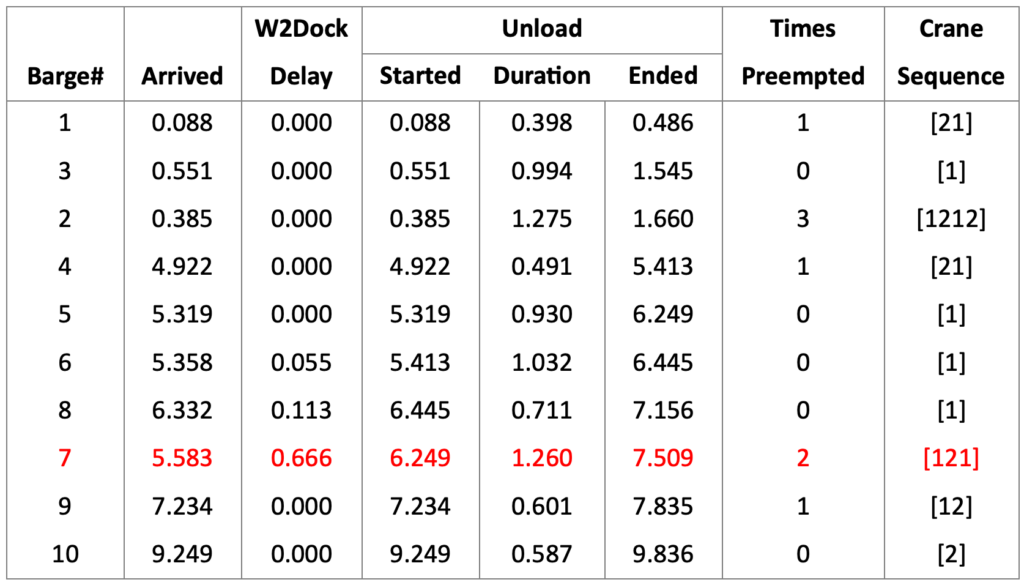
Table 1 shows example simulation results for the first ten Barges that arrived at the harbor to unload. The times for the Arrival and Unload events, the waiting times in queue W2Dock, and the total duration needed by each Barge to unload, are shown in days. The unloading of Barge 7 that started at 6.249 with 1 Crane is an example of instance Unload(x+2) (described above). The entire unloading of Barge 8 that started with 1 Crane later at 6.445 but finished first at 7.156 is an example of Unload(x+3). Because Barge 9 arrived later at 7.234, after Barge 8 had finished, the departure of Barge 8 at 7.156 is an example where the appropriate instance to preempt for Barge 7 was not the last but the next-to-last instance Unload(x+2). This allowed Barge 7 to start Unload(x+4) at 7.156 with 2 Cranes. Later, at 7.234 the arrival of Barge 9 preempted Unload(x+4) so that Barge 7 could start Unload(x+5) and Barge 9 could start Unload(x+6) both with 1 Crane. Thus, Barge 7 was preempted 2 times and the sequence of cranes that unloaded Barge 7 was [121].

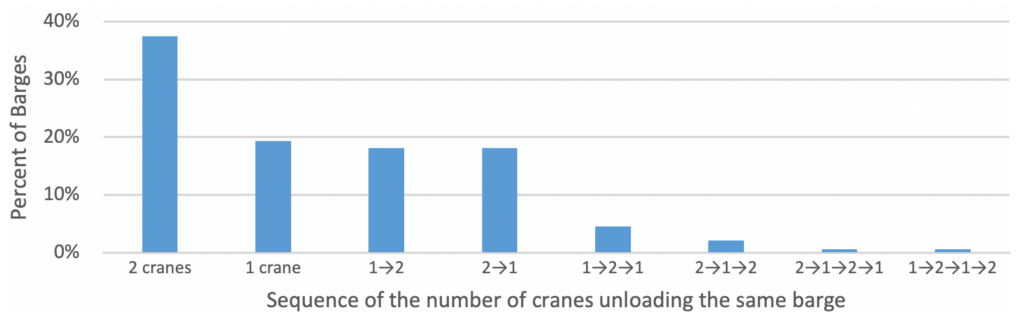
The histogram in Figure 4 shows the percentage of barges that were unloaded by each possible sequence of cranes working alone or together. The first two columns show that unloading 56% of the barges was not preempted, with 37% of the barges using two cranes from start to finish while 19% used just one crane. The rest of the columns show that the remaining 44% of the barges were preempted up to three times. For example, about 18% started unloading with one crane, were preempted, and finished unloading with two cranes (1→2). About 4% of barges started unloading with one crane, were preempted and continued with two cranes, and were preempted again and finished with one crane (1→2→1). And about 1% of the barges were preempted three times and followed the sequence (2→1→2→1) or the sequence (1→2→1→2).

As this example clearly illustrates, modeling all possible sequences of cranes by which a barge may be unloaded while keeping track of its remaining unload time can be quite challenging. The new STROBOSCOPE functions and statements that support preemption directly at the system level make it easier to develop reliable models that implement preemption correctly.

Conclusion

Construction simulation models often need to interrupt activities when triggering events occur, such as when differing soil conditions are encountered, when inclement weather occurs, or when equipment arrives or breaks down [4], [5]. As the above examples illustrate, prudent activity preemption can also be used to improve the design of operations and to increase production or reduce waiting and service times. The models presented in this paper can serve as examples that illustrate how to use the new preemption facilities added to STROBOSCOPE to tackle these situations directly and to model preemption in general. The complete STROBOSCOPE models for the two examples presented are available from the author.

References

1. A. M. Law, Simulation Modeling and Analysis, 5th ed. Dubuque: McGraw-Hill, 2014. [Online].
   Available: www.mheducation.com/highered/product/simulation-modeling-analysis-law/
   M9780073401324.html
2. J. C. Martinez and P. G. Ioannou, “STROBOSCOPE Simulation System Software.” University of Michigan, Ann Arbor, Michigan, 2023. [Windows]. Available: Retrieved from www.ioannou.org on March 15, 2023
3. J. C. Martinez, “STROBOSCOPE State and Resource Based Simulation of Construction Processes,” PhD dissertation, University of Michigan, Dept. of Civil Engineering, Ann Arbor, Michigan, 1996. [Online]. Available: https://www.ioannou.org/publications/umthesis
4. P. G. Ioannou and J. C. Martinez, “Comparison of Construction Alternatives Using Matched Simulation Experiments,” Journal of Construction Engineering and Management, vol. 122, no. 3, pp. 231–241, Sep. 1996, doi: 10.1061/(ASCE)0733-9364(1996)122:3(231).
5. P. G. Ioannou and V. R. Kamat, “Intelligent Preemption in Construction of a Manmade Island for an Airport,” in Proceedings, Winter Simulation Conference 2005, Orlando, Florida, Dec. 2005, pp. 1515–1523. doi: 10.1109/WSC.2005.1574419.